
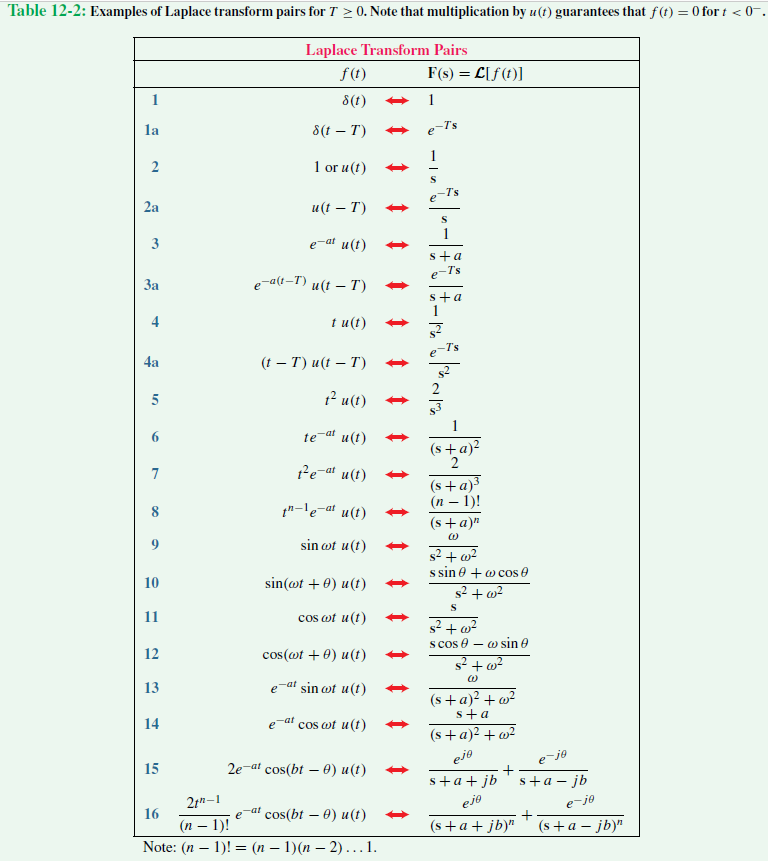
But notice that your table may or may not contain all of the possible Laplace transformations that you need, this can occur due to the type of function that is given to you in a problem. So far, we have only used the comparison method to solve the Inverse laplace transform examples, but this is just the tip of the iceberg! For practical purposes we usually have a table (such as table 1) at hand to solve problems quickly. Make sure your answer contains all the proper factors and values for "a", "b" and "n" Find the answer by looking into the function f(t) on the table that gave as a result the F(s) which is similar to the F(s) in your problem.Ħ.
Take the inverse Laplace transform of your simplified function. Factorize terms out of your given F(s) in a way that the function left is as similar as possible to the F(s) in the tableĥ. Identify terms such as "a", "b" and "n" on the given function in relation to the formula on the table, and find their values.Ĥ. Look at the Laplace transform table and identify a F(s) equation similar (with similar denominator) to the given F(s) in your problem.ģ. If there are more than one term in the given function, then repeat these steps for each of them.Ģ.
#LAPLACE TRANSFORM TABLE HOW TO#
Check how many terms does the function have, if only one, then the next steps explain how to obtain the inverse Laplace transformation of it.

F(s) is always the result of a Laplace transform and f(t) is always the result of an Inverse Laplace transform, and so, a general table is actually a table of the transform and its inverse in separate columns.Įquation for Example 2(d):Putting together the answers to find the final Inverse Laplace transform solutionĪfter solving two examples, is time for us to list the steps to follow in order to obtain the Inverse Laplace transform of a given function F(s) with the method of table comparison:ġ. A general table such as the one below (usually just named a Laplace transform table) will suffice since you have both transforms in there. In order for us to follow our intuitive and practical method of comparison, we have included a table of the most common Laplace transformations.Ī nice detail to notice is that you do not need a particular Inverse laplace transform table if you want to solve problems of this type. How to find the inverse laplace transform: It is imperative you have knowledge on calculating Laplace transforms so the terms and methodology on this article are meaningful to your studies. We will call this method "the comparison method" or "table comparison method" and we will show you how to work through it step by step in the next section.īefore you continue, make sure you have had an introduction to the Laplace transform or take a quick review if it has been long since you studied it. On this article we will focus on this practical approach of solving the Inverse Laplace transformation, which uses a Laplace transform table as aid. Formula 2: Inverse Laplace transform general integral formĪlthough the inverse Laplace transform formula may seem intimidating, we will be showing there are much easier methods to obtain the result for the inverse transform of a function.


 0 kommentar(er)
0 kommentar(er)
